CÓNICAS

Se entiende por CÓNICAS o SECCIONES CÓNICAS a las curvas planas que se producen por la  intersección de un plano con un cono.
Las intersecciones del plano con el cono dependen del modo como éstas se produzcan. Cambiando el ángulo del plano y el lugar donde éste corta al cono, se producirán secciones diferentes.

En el siguiente dibujo tienes una cartulina amarilla que “corta”

perpendicularmente al eje del cono y compruebas que la sección es el círculo en azul, siempre que el corte no se produzca por el vértice. Su contorno es una circunferencia.
Estudiaremos su contorno, es decir, la circunferencia.

    ECUACIÓN ORDINARIA  (x ─ a) 2 + (y ─ b) 2 = r 2

Si el plano corta oblicuamente al eje del cono y a todas sus generatrices, sin pasar por el vértice, la sección que obtenemos es una elipse.

Mantenemos la misma cartulina amarilla y la sección resultante en azul:

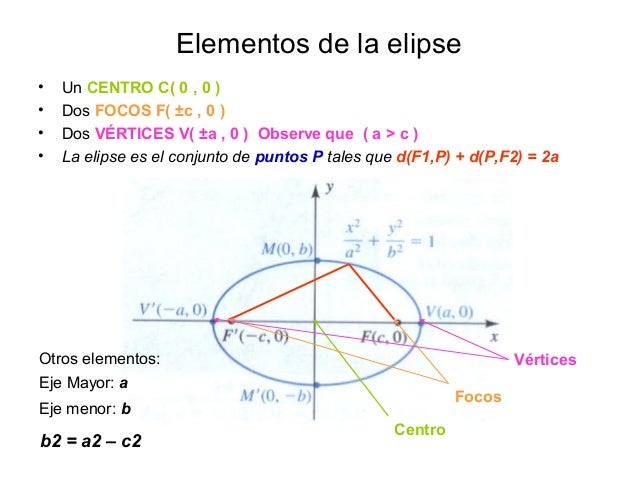
La ecuación de una elipse cuyo eje mayor es horizontal viene dada por:

(x−x0)2a2+(y−y0)2b2=1

Donde:

• x0 , y0 :  Coordenadas x e y del centro de la elipse
• a : Semieje de abcisas
• b : Semieje de ordenadas. En nuestro caso debe cumplirse que b ⩽ a.

Si el corte lo hacemos, de forma oblicua al eje del cono pero paralela a la generatriz del mismo  obtenemos una parábola:

ecuación de la parábola en su forma ordinaria o canónica

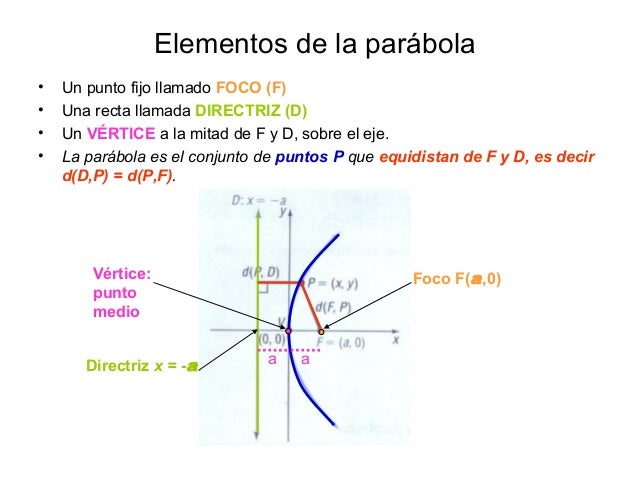
y 2 = 4px

Si el plano corta a las generatrices en ambos lados del vértice del cono, obtenemos una hipérbola.

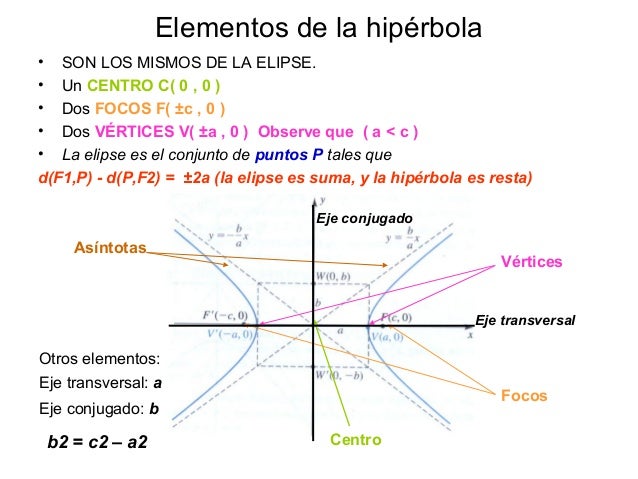
Ecuación reducida de la hipérbola

Si te fijas en la figura siguiente, a las cónicas podemos clasificarlas teniendo en cuenta el ángulo que forman el plano con el eje del cono:

Si el plano es perpendicular al eje, tenemos una sección circular cuyo contorno es la circunferencia.

Si el ángulo que forma el plano con la base es menor que el ángulo que forma el plano con la generatriz, tenemos que la sección será una elipse.

Si el plano es paralelo a la generatriz tenemos la parábola.

Si el ángulo que forma el plano con la base es mayor del que forma con la generatriz, tenemos la hipérbola.